Overview

In an environment of low interest rates and a steep yield curve (the spread between short and long-term interest rates), investors can obtain an above-market yield by betting against the market. A steep yield curve indicates that the market anticipates higher interest rates in the future. If an investor has confidence that interest rates will not rise as far or as fast as the market predicts, and the investor is correct, then the investor can obtain an enhanced return by investing in a range accrual note.

A range accrual note (also called an accretion bond index range note; corridor bond or note; range floater; accrual note; LIBOR range note; range accumulation note; or a fairway bond) is a structured product where the coupon is linked to the performance of a reference index, for example, the six-month USD LIBOR. The return from the note will be higher than that from traditional fixed-rate deposits if the spot six-month USD LIBOR moves within a pre-determined range during the life of the note.

For example, suppose an investor wishes to enhance the yield on a portfolio of short-term investments. And suppose it is the investor's opinion that LIBOR will continue trading around the current level. The investor buys a range accrual note, for which a target range of the spot six-month USD LIBOR is defined. The investor is taking the view that the underlying spot six-month USD LIBOR will stay within the range. Each coupon depends on the number of days in the coupon period that the spot six-month USD LIBOR fixes within the pre-determined range. Interest is accrued at an above-market rate on each day that the underlying rate fixes within the range, and no interest is accrued on each day that the underlying rate fixes outside the range.

Investors therefore potentially obtain an above-market return by exposing themselves to interest rate risk. In an environment of low interest rates, this risk may be acceptable because most notes are 100% capital protected upon maturity, in which case the investor faces only coupon risk and not principal risk. Investors can obtain an even higher return by adding more risk to the structure: by making the note callable. A callable range accrual note is a range accrual note where the issuer has the option to call the note at specified dates in the future, typically at par. For example, if the investor has predicted movements in the reference rate correctly and is obtaining high return, then the issuer has the right to call the note and return the principal to the investor. This option is valuable to the issuer and exposes the investor to re-investment risk. The issuer offers the investor a higher potential return in order to compensate the investor for this additional risk.

Callable range accrual notes typically start as range accrual notes that offer a high initial coupon. After an initial period, the coupons become dependent on whether or not the reference index stays within the pre-determined range. After an initial "lockout" period, the notes become callable on coupon payment dates. When the note is called, the investor receives the principal back and stops receiving coupons. The benefit of these structures for investors is that they get an above-market initial coupon and potential above-market coupons in the future if the reference rate stays within the pre-determined range. Also, investors benefit from diversified risk, because each coupon depends on daily rate observations instead of a single rate fixing. For their part, issuers have an option to cancel the note that can be very valuable. The issuer delta- and vega-hedges the note throughout its life with the intention of recouping the initial high coupon payments as hedging profits. A risk for the investor, then, is that it is possible to get stuck with an investment that pays little or no coupon over the life of the note. This life can be long, because (callable) range accrual notes with attractive potential coupons are typically long-dated instruments. Another risk for the investor holding a callable range accrual note is that the principal will certainly be returned early and the coupons stopped if the investor forecasts the reference rate correctly and the coupons are large.

FINCAD Valuation

The FINCAD XL 8.1 and FINCAD Developer products provide functions that calculate the fair value and risk statistics of bermudan range accrual notes with both call and put options and a user-defined exercise schedule. The notes may have time-varying notional, fixed coupon rate, and accrual rate ranges.

Separate functions are available for valuing range accrual notes vs. callable range accrual notes. The FINCAD functions for valuing range accrual notes can be used to value the accrual leg of a range accrual swap. The FINCAD functions for valuing callable range accrual notes can be used to value callable range accrual swaps, provided there is no spread on the floating leg of the swap. If there is a spread, then the FINCAD functions can still be used to value the swap although an approximation is required.

To download the latest trial version of FINCAD Analytics, contact a FINCAD Representative.

Range accrual notes are valued by replicating the payoff in terms of a sum over daily floorlets struck at the lower and upper rate boundaries of the accrual range. Because floorlets must be valued at two different strikes per coupon period, Range accrual notes are skew-dependent instruments. The floorlets are valued using a stationary one-factor short rate model (Hull-White or Black-Karasinski) or the Black model [1]. Volatility "smile" or "skew" structure is taken into account by calibrating the model parameters to the market prices of caplets and/or floorlets that expire on rate observation dates and are struck at the accrual range rate boundaries. For example, given a short rate model calibrated separately to caplets and/or floorlets of different expiry and strike, the range accrual note valuation function uses the short rate volatility and mean reversion parameters appropriate to the expiry date and strike of each floorlet being valued.

Callable range accrual notes are valued using a model that attempts to match both the market prices of swaptions and floorlets. The approach is to use a simple model to match diagonal swaption prices, and then use "internal adjusters" to match the volatility smile structure of floorlets [2, 3].

The callable notes are valued on a trinomial interest rate tree, which is built using a stationary one-factor short rate model (Hull-White or Black-Karasinski) calibrated to diagonal swaptions. In the limit of a very wide accrual range, the price of the callable range accrual note should then approach that of a callable fixed-rate bond. The valuation procedure for a callable range accrual note should also reproduce today's market value of each coupon. For example, if there is a 25% chance of calling the note before the jth coupon date (i.e., there is a 75% chance of not calling the note before the jth coupon date), then the valuation procedure should give 75% of the vega risk of the floorlets that make up the jth coupon. This means that the valuation procedure should use the correct market volatilities for the floorlets struck at the rate boundaries of the accrual range. The valuation procedure for callable range accrual notes achieves consistency with the market prices of both swaptions and floorlets by:

• Building a tree using today's yield curve and the model parameters calibrated to diagonal swaptions struck at the money. These model parameters determine the yield curve at each node on the tree, and the node-node probabilities.
• "Internally adjusting" the model parameters at each tree node for the purpose of valuing the floorlets that make up each future coupon. That is, the floorlets are valued using model parameters calibrated to caplets and/or floorlets with expiry dates at or near the future rate observation dates, and strikes at or near the accrual range rate boundaries.

Example

Suppose we have a deal sheet for a callable range accrual note that we wish to value. Specifically, we wish to value a USD 5-year callable range accrual note, indexed on 6-month LIBOR, with a quarterly coupon.

• The coupon is 7% x AF, where AF = accrual factor = In_Days/Period_Days.
• In_Days = number of calendar days in the relevant Observation Period on which the Underlying Reference is strictly at or lower than the Upper Bound and is strictly at or higher than the Lower Bound.
• Period_Days = number of calendar days in an Observation Period.
• The Lower Bound is 0%, and the Upper Bound varies with time as shown in the Figure below.
• For every Observation Period, the daily observation starts 2 Business Days prior to the beginning of each interest period, and ends 2 Business Days prior to the end of the interest period. Prior observation will be used for non-Business Days.
• The Business Centre is London for both rate observations and payments.
• The Day Count Convention is 30/360, Modified Following Business Day.
• The Issuer has the right to call this note at par plus accrued interest after 3 months from Issue Date, and every 3 months thereafter, with a minimum of 5 business days of notification.
• The Settlement Date is 1 month prior to the Effective Date, which is March 14, 2000.

We will value the callable range accrual note using the Hull-White short rate model. Suppose we have calibrated this model four times: (1) to at-the-money MxN diagonal swaptions, where M+N = 5 and the maturity date of the swaptions is the same as the maturity date of the callable range accrual note; (2) to 6-month caplets expiring on March 14, 2003, struck at 2%; (3) to 6-month caplets expiring on March 14, 2003, struck at 5%; and (4) to 6-month caplets expiring on March 14, 2003, struck at 8%.

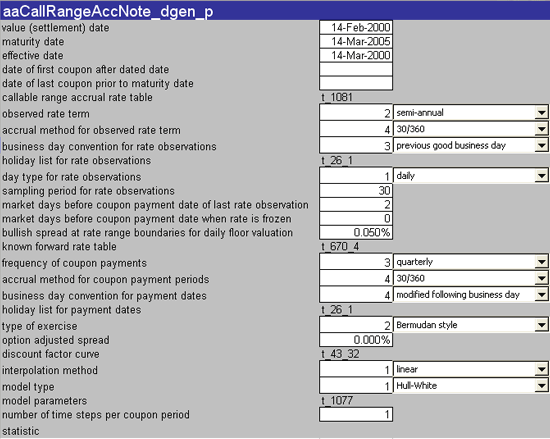
Below is a screenshot of a spreadsheet using aaCallRangeAccNote_dgen_p in FINCAD XL Version 8.1.

[1] Hull, John C. Options, Futures, & Other Derivatives, Fourth Edition, Prentice-Hall, Inc., Upper Saddle River, NJ, 2000.

[2] Hagan, Patrick S. "Adjusters: Turning Good Prices into Great Prices", The Best of Wilmott, Volume 1, John Wiley & Sons, Ltd, England, 2005.

[3] Hagan, Patrick S. "Accrual Swaps and Range Notes", Bloomberg Finance LP* (Unpublished).

Disclaimer

Your use of the information in this article is at your own risk. The information in this article is provided on an "as is" basis and without any representation, obligation, or warranty from FINCAD of any kind, whether express or implied. We hope that such information will assist you, but it should not be used or relied upon as a substitute for your own independent research.

For more information or a customized demonstration of the software, contact a FINCAD Representative.

* Bloomberg is a trademark of Bloomberg Finance LP. FINCAD is not associated in any way with Bloomberg Finance LP.