To view FINCAD workbooks that value employee stock options (ESOs), contact a FINCAD Representative to download the latest trial version of FINCAD Analytics

1. Introduction

An employee stock option (ESO) is an option granted by a company to an employee, which gives them the right to buy a pre-specified number of the company's shares during some period of time. However, an ESO is characterized by some key features which make it very different to a standard American exercise option.

Before one studies the implementation of any particular model, it is useful to note the general features of an ESO.

1. Delayed Vesting

   An ESO that is granted at time t = t₀ and expires at time t = T cannot be exercised until time t = v, such that t₀ v T. The period of time v - t₀ is called the vesting period of the option.

   • During the vesting period, the ESO cannot be exercised. If the employee leaves the company for any reason, the option is forfeited.
2. Exercise Features

   After the vesting period, if the employee leaves the company for any reason:

   • The option must be exercised immediately if it is in-the-money.
   • The option is forfeited if it is out-of-the-money.

   On the other hand, if the employee remains in the firm:

   • The option can be exercised at any time, but cannot be sold. If the employee needs cash or wants to diversify their portfolio, they must exercise the ESO and sell the underlying share. Because of this, ESOs are typically exercised earlier than similar traded options.

2. Modeling ESOs: Some Key Parameters

In order to model some of the characteristics mentioned above and their implications, FINCAD's implementation of an ESO involves the following concepts, which are based on the binomial tree model as described in [1] and [2] .

a) Exercise Multiple

An exercise multiple, M is introduced to capture the early exercise feature of ESOs. It is not observed in the market, but should be thought of as being estimated by the company based on historical records of the observed exercise practices of its employees [ref HW]. The exercise multiple conveys information regarding the average 'in-the-moneyness' of the historically exercised options as a multiple of the strike-price, K. In HW's enhanced model, an option is necessarily exercised once S_t ≥ KM. In the binomial tree model of HW, this means that the option is exercised on all nodes with S_t ≥ KM. In particular, for those nodes with S_t = KM, the payoff is:

S_t - K = KM - K = K(M - 1).

Such nodes effectively act as a boundary in the binomial tree, since all nodes with values greater than KM are automatically exercised. This model feature gives rise to two counteracting forces acting on the value of the ESO:

• The payoff on each such node increases as M increases.
• However, the likelihood of exercise on each such node is lower, since S_t becomes increasingly less likely to cross the KM threshold.

FINCAD's implementation of HW's model allows for a time-dependent exercise multiple.

b) Exit Rate

An exit rate, e, is introduced to model the proportion of employees who leave the firm: a probability eδt exists that the employee leaves the company during the time period δt, with e being the continuously compounded employee exit rate per year.

After the vesting period:

For nodes with S_t ≥ KM, the exit rate is irrelevant.

For nodes with S_t KM, the exit rate affects the value of each node negatively: as more employees leave, the ESO will be worth less, since it may well have to be forfeited. However, even if the exit rate is set to 100% (all employees leave the firm), it is still possible to get a value for the option, since there is a chance that the ESO will be in-the-money, and so exercised, when the employee leaves.

FINCAD's implementation of HW's model allows for a time-dependent exit rate.

c) Barrier

FINCAD has also added an extra feature to the HW model, namely a standard knock-in barrier. After granting an ESO with such a barrier, the option will become alive only if the underlying spot price, S_t, crosses the barrier value, B. If the underlying price does not breach the barrier during the lifetime of the option, then it will simply expire worthless.

2. Payoff on the Binomial Tree

Following [1] and [2], ESOs are valued on a Cox-Ross-Rubinstein binomial tree. It is important to note the payoff structure on each node of the tree:

For an American option:

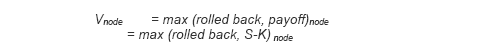
For an ESO:

Here, rolled back refers to the standard practice of rolling back values from a (t+1)^th nodes to a t^th node by the use of risk neutral probability measures that govern the up- and down-tick in a binomial tree along with the risk free interest rate. (See [4] for more details) For an ESO, the rolled back amount also involves an exit rate. (See [5])

3. ESO vs European Options

Intuitively, one might expect the following. Upon increasing the vesting period, the ESO valuation must approach the value of the European Option, ceteris paribus. If the vesting date equals the option maturity date, the ESO will be worth the same as the corresponding European option.

Using FINCAD's aaESO_HW_enhanced2_p( ) function, we see the following results.

Parameters	aaESO_HW_enhanced2_p	aaBSG
Underlying Price	47	47
Strike Table	40	40
Expiry Date	2/14/2010	2/14/2010
Value Date	2/14/2000	2/14/2000
Vesting Date	2/13/2010
Volatility Table	20%	20%
Exit Table	0%	0%
Exercise Multiple	1
Barrier Table	0
Risk Free Curve	5%	5%
Holding Cost Curve	4%	4%
Time Steps	2000
Fair Value	11.13	11.13

As the calculations show, the European option and the ESO converge in value using this simple adjustment of the vesting periods.

4. ESO vs American Options

In contrast, using aaBIN2( ) function which values an American option, one might anticipate that by decreasing the vesting period the value of the American exercise and an ESO value might converge.

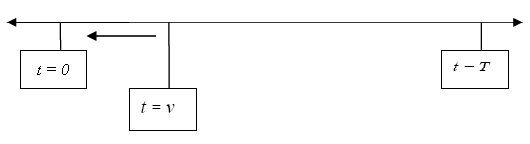
However, this is not the case. The key issue to realize is that unlike an American option, the above model of ESO often results in a suboptimal exercise (capturing the early exercise features mentioned in 1(b)).

On the binomial tree, an American option is valued by rolling back the values through the tree and comparing them with what the holder would get upon exercise. If it is optimal to exercise on any node, then the fair value of the option on that node is just the payoff.

Consider a contract with the following tree-diagram for the evolution of stock prices over four time periods.

Here, S₀ = 8, K = 8, M = 1.1, σ = 10%, risk free rate = 5%, holding cost = 5%, time steps = 4, and the calculated probability of an uptick in the stock is p = 0.48231. The vesting date is set to zero, and the tenure of the option is two years.

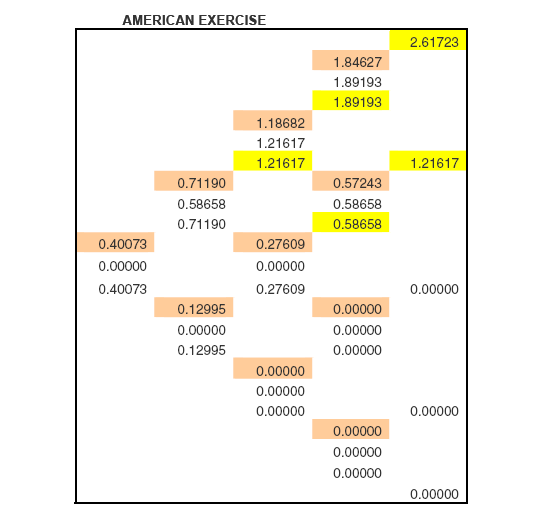
In the case of an American option, the resulting option value is given as in the diagram below. Here, the dark-orange cells are the values on each node, derived by rolling back the option value from the nodes at the later time-step. The actual option value on each node, however, is given by:

Max( Roll Back Value, Payoff )

An exercise is made at that node if and only if, Payoff > RollBack Value . In the diagram below, the cells in yellow indicate the nodes where it is optimal to exercise.

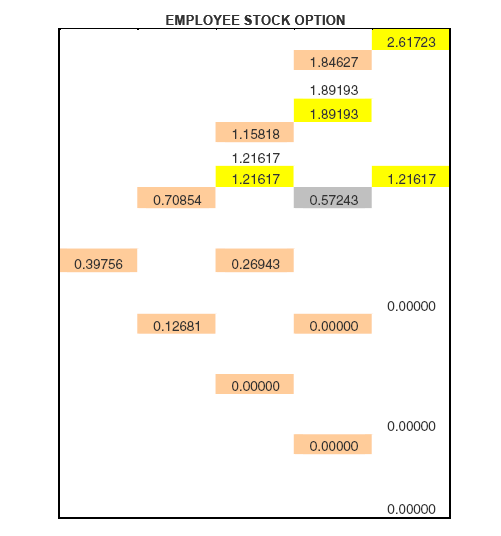
In contract, for an ESO, if any node has S_t ≥ KM then the option is necessarily exercised on that node, even if it is not optimal to do so. The option is always worth the payoff on such nodes.

In essence,

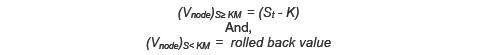
In the above example, the exercise multiple = 1.1. Therefore, on all nodes in the tree with S_t ≥ 1.1*K = 8.8, the option will be exercised. The nodes with S_t= 8.8 (or the nodes closest to that line) act like a boundary in these trees. Nodes with S above that line do not affect the value of the option: since it is always exercised when S_t ≥ K, the option value is always reset to equal the payoff. This is very different to the American case, when the option value is overwritten only when it is optimal to do so.

In the diagram below, the cells in yellow are the nodes on which the ESO is exercised. Note the cell in gray with a value of 0.5723. In an American option, that node is also exercised but in an ESO that node is not exercised. Intuitively, this implies that should the stock arrive at 8.58658 at t = 0.75, if one were owner of an American option, the option would be exercised. If one were instead holding an ESO, the barrier condition implies that the option would not be exercised.

4. Conclusion

Although an ESO might superficially resemble an American option, its exercise features mean that it is in fact very different. Some scrutiny of the HW model - which captures these exercise features - shows the differences explicitly. The primary issue is that for ESOs, exercise is forced, whereas for American options, exercise is optional.

References

1. Hull, John C., Hull, J. C. and White, A. (2004) 'How to Value Employee Stock Options', Financial Analysts Journal, 60, 1 114-119.

2. Hull, J. C. and White, A. (2004) 'Accounting for Employee Stock Options: A Practical Approach to Handling the Valuation Issues', Journal of Derivatives Accounting, 1, 1 3-9.

3. Rogers, L.C.G & Scheinkman, J. (2006) 'Optimal Exercise of American Claims When Markets Are Not Complete', Unpublished Manuscript, Available at: http://www.princeton.edu/~joses/wp/OEAC.pdf

4. Shreve, Steven E. (2005) `Stochastic Calculus for Finance: The Binomial Asset Pricing Model', Springer Verlag, New York.

5. "Employee Stock Options", Technical Document accompanying FINCAD XL v9.1.

Disclaimer

Your use of the information in this article is at your own risk. The information in this article is provided on an "as is" basis and without any representation, obligation, or warranty from FINCAD of any kind, whether express or implied. We hope that such information will assist you, but it should not be used or relied upon as a substitute for your own independent research.

For more information or a customized demonstration of the software, contact a FINCAD Representative.