FINCAD Analytics Suite now offers support for calibrating the Heston model of stochastic volatility, and for pricing European options, variance and volatility swaps within this model. The Heston model is an industry standard model which can account for the volatility smile seen in the market. The FINCAD Analytics Suite functions introduced in 2008 allow fast pricing of European options, variance and volatility swaps, necessary for calibration routines; the calibration itself; calculation of the Greeks, including sensitivities to the Heston model parameters; and calculation of the implied volatility surface for a given set of such parameters.
» Click to evaluate the lastest trial version of FINCAD Analytics Suite!
Overview
Despite its tremendous success, the Black-Scholes model of option pricing has some well-known deficiencies, perhaps the most important of which is the assumption that the volatility of the return on the underlying asset is constant. In reality, the implied volatilities of traded options generally vary, both with strike price and with maturity of the option. The variation with strike price is called the volatility smile, or the volatility skew.
The question then arises as to how to price options in a way which is consistent with this market-observed variation of implied volatility. One of the concepts used to cope with this problem is that of stochastic volatility. There are various models of stochastic volatility, although arguably the most popular is the Heston model [1].
The constant volatility of the Black-Scholes model corresponds to the assumption that the underlying asset follows a lognormal stochastic process. On the other hand, the basic assumption of stochastic volatility models is that the volatility (or possibly, the variance) of the underlying asset is itself a random variable. There are two Brownian motions: one for the underlying, and one for the variance; stochastic volatility models are thus two-factor models. Of course, the two processes are correlated and, at least in the equity world, the correlation is usually taken to be negative: increases/decreases in the asset price tend to be coupled to decreases/increases in the volatility.
Once the variance of the underlying has been made stochastic, closed-form solutions for European call and put options will in general no longer exist. One of the attractive features of the Heston model, however, is that (quasi-) closed-form solutions do exist for European plain vanilla options. This feature, in turn, makes calibration of the model feasible.
The implied volatility of such a European option is then the value of the volatility which would have to be used in the Black-Scholes formula, to get that specific price. By varying the strike price and maturity, one can thus back out the implied volatility surface for the specific set of Heston model parameters under consideration. One finds that the Heston model gives rise to a wide variety of implied volatility surfaces, many of which capture market-observed behavior very well.
Pricing European Options in the Heston model
The Heston model has five independent parameters, all of which can be determined by calibrating to the market-observed prices of European options of various strikes and/or maturities. Once a set of parameters has been determined in this way, one can price other options, say a European option of a different strike, an American option, or a more exotic product.
The underlying asset price follows a standard lognormal process, and the variance V follows a mean-reverting square root process:

where
 is the risk-free interest rate, we have ignored dividends &
is the risk-free interest rate, we have ignored dividends &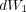 and
and  are two (correlated) standard Brownian motions.
are two (correlated) standard Brownian motions.- The five Heston model parameters are:
- the initial variance
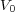
- the long-term variance
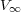
- the speed of mean reversion

- the volatility of volatility
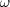
- and the correlation
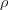
- the initial variance
In General, the price at time 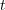 of, say, a a European call option maturing at time
of, say, a a European call option maturing at time 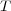 is given by the discounted expectation value
is given by the discounted expectation value
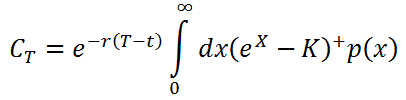
where  and
and 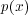 is the probability density function of the underlying logarithmic asset price.
is the probability density function of the underlying logarithmic asset price.
Since analytic forms for such option prices cannot always be derived, it often turns out to be useful to work with the characteristic function
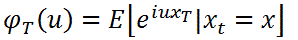
which is just the Fourier transform of the probability density function from x-space to u-space. To price plain vanilla European options, one can use the characteristic function in different ways. We choose to use the fast Fourier transform technique of Carr & Madan [2]. The beauty of this technique - apart from its speed - is that the prices of options with a range of strikes are computed all at once. Moreover, with a little thought, the technique can also be extended to put options and binary options, as described in [3].
The functions introduced in 2008 can price European plain vanilla options, portfolios of such options, some common trading strategies, and options with arbitrary piecewise linear payoffs. They also return the sensitivities to all the Heston model parameters, in addition to the standard Greeks.
Calibrating the Heston model
The Heston model parameters can be determined by calibrating to a market observed implied volatility smile for European options. The calibration routine takes as its starting point the implied volatilities for a set of such options, with varying strikes and/or maturities. The volatilities are converted to option prices, and the parameters of the Heston model are chosen so as to best match this set of market data.
All calibration algorithms search a region of parameter space in a more or less intelligent way, by minimizing an error metric. For a given set of parameters, the prices of the relevant options are computed using the Heston model pricing methodology. The error metric is then calculated. This is just a way to measure the discrepancy between the market data and the option prices predicted by the model with a given set of parameters. The smaller the error metric, the closer the predicted prices are to the market data. The next trial set of parameters are then chosen according to how the error metric has changed, and the process begins again.
The calibration function takes a set of parameter ranges and a set of initial parameter values. The routine starts with the set of initial parameters, and searches the region of parameter space specified by the parameter ranges, in order to minimize the error metric. The user thus has control over what range of parameters to look at for a given set of market data and can also, for example, use a previous set of calibrated parameters as a starting point for a future calibration.
FINCAD Analytics Suite provides the choice of three calibration algorithms (Levenberg-Marquardt, downhill simplex and differential evolution) and also the choice of three error metrics. In addition to this, different weights can be assigned to each individual option in one of three ways. The user might want to assign less weight to data for illiquid out-of-the-money options, for example, and more weight to the liquid at-the-money options.
The differential evolution algorithm is most likely to find the best set of parameters for a given set of option prices, but the algorithm can take a significant amount of time to finish its search. For that reason, the calibration function returns an order-of-magnitude estimate for the length of time it will take. One recommendation is to use the differential evolution algorithm periodically and, at least if the market data have not changed too much, to use the Levenberg-Marquardt algorithm on a more frequent basis. The results of the differential evolution algorithm can then be used as the set of initial parameter values for the Levenberg-Marquardt routine.
Example
In this example, we calibrate the Heston model to options market data, and then use the calibrated model to price a European binary call option. We use the FINCAD Analytics Suite workbook European Option (Heston Model), with options data from 1-Jan-2007 entered in the worksheet Options Data as shown in the screenshot below.
Both bid and ask volatilities for options of various expiry dates and strike prices are entered. The volatility uncertainties are calculated as the bid-ask spread and the mid volatilities are used in the calibration routine. This is performed in the worksheet Calibration to Options as shown below.
Imagine that we have calibrated this model to options data just a little while ago, using the differential evolution error minimization method. Imagine also that the options data has not changed much since then. So in this case, we choose Levenberg-Marquardt as the error minimzation method, with the initial model parameters (in the Initial Model Parameter Table) taken to be the results of the previous calibration (with differential evolution). We choose a fairly wide range of model parameters (in the Model Parameter Range Table) and calibrate the model.
The overall calibration result is rated GOOD by the calibration checklist on the worksheet Calibration Check. The checklist tests various criteria in order to classify a calibration as INADEQUATE, ADEQUATE, or GOOD. The checklist for the present calibration is shown in the following screenshot.
We can also check the calibration visually by clicking the Error Analysis button, which will bring up plots of the datapoints and the predicted values, for both price and implied volatility.
Now that we have a calibrated model, we can use it to price various derivatives. Here we will consider pricing an at-the-money European binary call option, which is set up as in the Main worksheet as shown below:
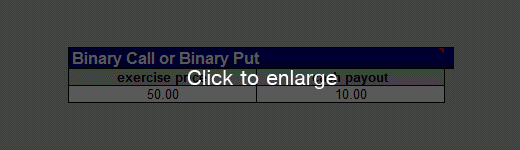
The strike and payoff of the binary call option are set up in the Strike Tables worksheet. We choose an exercise price of $50 and a cash payout of $10:
Strike Table
We also choose the parameter source to be calibration to options, so that we are using the calibrated model parameters. Calculating the option price and risk statistics shows that this option is worth a little over $5.
Finally, we can see what implied volatility surface this calibrated model gives rise to. The details are set up in the Implied Volatility Smile worksheet as shown below:
The Expiry Date & Exercise Price Settings dictate which exercise date and strike prices to show on the implied volatility surface. Both the surface itself and cross sections of the surface for different expiry dates are shown in the Graphs worksheet:
Summary
The FINCAD Analytics Suite functions described here allow the user to calibrate the Heston model of stochastic volatility and to use that calibrated model to price various European options, variance and volatility swaps. They also allow the user to view the implied volatility surface which the Heston model gives rise to.
References
[1] Heston, S. (1993) 'A closed-form solution for options with stochastic volatility', Review of Financial Studies, 6, 327-43.
[2] Carr, P. and Madan, D. (1998) 'Options Valuation using the Fast Fourier Transform', Journal of Computational Finance, 2, 61-73.
[3] Lee, R. W. (2004) 'Options Pricing by Transform Methods: Extensions, Unifications, and Error Control', Journal of Computational Finance, 7, 51-86.
Disclaimer
Your use of the information in this article is at your own risk. The information in this article is provided on an "as is" basis and without any representation, obligation, or warranty from FINCAD of any kind, whether express or implied. We hope that such information will assist you, but it should not be used or relied upon as a substitute for your own independent research.
» For more information or a customized demonstration of the software, contact a FINCAD Representative.