In my previous post (Part 4) of this series I explained how the index concept relates to complex payoffs. In this post I will define some higher-level Product types, all still Products, but with some specific structural features that makes expressing common derivatives convenient.
Leg
A Leg consists of a collection of Flows, all made in the same direction and in the same currency. It is the generalization of a single Flow to the idea of Flows made on a schedule. Such a schedule may be generated from functionality within the library, but schedule generation is a separate problem and the construction process for an object representing a Leg should consume a schedule, not instructions for generating one. A further concept that is most readily associated with a Leg is that of a notional structure; a collection of notional amounts, one per Flow, that varies in time.
Swap
A Swap consists of two Legs, with payments made in opposite directions. Swaps are very common structures and so having an explicit concept for them is of great utility. It facilitates the calculation of quantities specific to swaps such as a par rate or margin. Note that this concept covers all types of swaps, from vanilla interest rate swaps or basis swaps to credit default swaps, cross-currency swaps or swaps with exotic payoffs. The distinguishing feature of these different types of Swaps is the nature of the amounts that are paid in each constituent Flow. The definition of payment amounts is covered in detail in an earlier post.
Portfolio
A Portfolio consists of a collection of Products. Note that a Portfolio is therefore also a Product and should have no special status in a valuation system. It should be valued on the same footing as all other Products and every calculation that works for an individual Product should also support Portfolios. A Portfolio of Flows (if in one currency) is equivalent to the corresponding Leg. A Portfolio of two offsetting Legs is equivalent to the corresponding Swap.
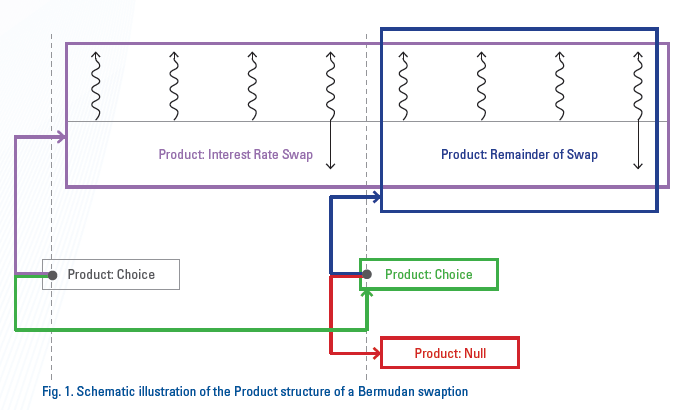
Choice
A Choice contains no payment obligations, only the right to make a single choice between two other Products. The payment direction indicator, introduced above in the context of a Flow, here indicates whether a party or their counterparty buys or sells the right to choose. A further Boolean value must indicate whether a given party chooses a given Product for themselves or for their counterparty to own. From the point of view of valuation, and assuming rational parties, this amounts to whether the highest or lowest value branch is selected. A choice between more than two alternatives can be constructed from the binary Choice described here, and so does not merit treatment as a separate Product type.
Conditional
A Conditional obliges a party to a contract to take ownership of one Product or another depending on some condition. The condition would be based on some quantities whose values can be observed unambiguously and agreed upon by all parties to the contract.
We have covered some useful subconcepts within the idea of a Product, but this is far from an exhaustive list. It is possible to construct higher-level structures such as that of the Bermudan swaption in Fig. 1, but this just amounts to further convenience; each such structure conforms to the definition of a Product and can be constructed using the above building blocks.
Next, I'll cover how the trading and ownership of physical assets fits into this cash flow focused framework.