In our last blog we reported on the relationship between the level of interest rates and their volatility. However, all of the data underlying the analyses that we reported on in that blog came from 2013 or earlier. Since then we have seen rates decline and, in many jurisdictions, become negative. In this blog we will discuss the models that can be used for calculating the price of European style interest-rate options such as caps and swap options when rates are low or negative.
There are four related models that can be used to calculate the price of European style interest-rate options such as caps or swap options. The most common model is Black’s model. In Black’s model the forward interest rate[1] follows the process
\[dF = \sigma F dz\]
where $dz$ is a Wiener process. In this model the future forward rates are lognormally distributed. The formula for the price of a call option on a rate is
\[\begin{gather}c = D \left[ FN \left( d_1 \right)-K N \left( d_2 \right) \right] \\d_1 = \frac{\ln\left( F/K \right)}{\sigma \sqrt{T}}+ 0.5 \sigma\sqrt{T}\\d_2 = \frac{\ln\left( F/K \right)}{\sigma \sqrt{T}}- 0.5 \sigma\sqrt{T}\end{gather}\]
where $K$ is the strike rate, $T$ is the time to option expiry, and $N$ is the cumulative standard normal distribution function. In the case of a caplet, $D$ is the value of a risk-free zero-coupon bond paying one dollar at the end of the period covered by the caplet multiplied by the length of the period in years to which caplet relates. In the case of a swaption, it is the value of a risk-free annuity that provides payoffs at the rate of \$1 per year on payment dates during the life of the swap. The option price is expressed as an interest rate. To turn it into a dollar value it must be multiplied by the principal amount underlying the option. The size of the volatility parameter, $\sigma$, is generally different for each option strike rate and each maturity. For options with a particular maturity the volatilities generally form a downward sloping smile: higher strikes have lower volatilities.
The second model is the Bachelier normal model in which the forward rate is normally distributed.[2] The diffusion process is
\[dF = \sigma dz\]
The formula for the price of a call option on a rate is
\[\begin{gather}c = D \left[ \left(F - K \right)N \left( d \right) + \sigma \sqrt{T} n(d) \right]\\d = \frac{F - K}{\sigma \sqrt{T}}\end{gather}\]
where $n$ is the standard normal density function. As with Black’s model, the size of the volatility parameter, $\sigma$, is generally different for each option strike rate and each maturity.
The third model is the constant elasticity of variance (CEV) model. The process for the CEV model is
\[dF = \sigma F^{\beta} dz\]
where $\beta$ must be between zero and two. The probability distribution for a future forward rate depends on the value of $\beta$. The option pricing model corresponding to the CEV model for $\beta >0$ involves the cumulative non-central chi-squared distribution.
The final model is the SABR model. This is a much more complicated model in which both the forward rate and the volatility of the forward rate are random. The process is
\[\begin{gather}dF = \sigma F^{\beta} dz\\d\sigma = \nu \sigma dw\end{gather}\]
where both $dz$ and $dw$ are Wiener processes. In this model, $\nu$ is the volatility of the volatility, the correlation between changes in the forward rate and changes in the forward rate volatility is $\rho$, and $\alpha = \sigma(0)$ is the initial volatility. Because it has so many volatility parameters ($\alpha$, $\beta$, $\nu$ and $\rho$) the SABR model can generally provide a good fit for all options with a particular maturity. It also reflects smile dynamics reasonably well. However, the volatility parameters are different for different option maturities. When choosing the volatility parameters to fit all options with a particular maturity $\beta$ and $\rho$ have similar effects. As a result, users generally select a value for $\beta$ such as $\beta = 0.5$ and then find the values for the other three parameters that best fit the observed prices. In the case of the SABR model there is a simple formula that allows the Black’s model volatility to be calculated approximately.[3] This calculated volatility is then used in Black’s model to calculate the option price.
These models are all closely related. Black’s model is a particular case of the CEV model with $\beta$ set to one. The Bachelier model is also a particular case of the CEV model in which $\beta = 0$, and the SABR model is equivalent to a CEV model overlaid with a stochastic volatility. The volatility parameters in these models have different meanings. In Black’s model $\sigma$ is the standard deviation of proportional changes in the forward rate. Typical values for $\sigma$, depending on the level of interest rates, are between 10% and about 100%. In the Bachelier model $\sigma$ is the standard deviation of changes in the forward rate. Typical values for $\sigma$ are between 0.2% and about 2%. For the CEV and SABR models the magnitude of the volatility parameter depends on the value of $\beta$. Higher values of $\beta$ are associated with higher values of $\sigma$.
For many years, the model used to price caps and swap options was Black’s model. The use of the model was so ubiquitous that until fairly recently brokers quoting prices for caps and swap options did so by publishing the Black volatility under the assumption that the customer would use this in Black’s model to determine the correct price for the option.
Now that interest rates have become very low or even negative it is no longer reasonable or even possible to use Black’s model since it does not allow negative rates. Of the four models only the Bachelier model allows rates to become negative. In the other three cases when rates may become negative it is necessary to modify the model by adding a shift, $s$, to the forward rate. For example, the shifted or displaced version of Black’s model obeys
\[d\left(F + s \right) = \sigma \left(F + s \right) dz\]
In this case $F + s$ is drawn from a log-normal distribution or $F$ is said to be drawn from a displaced log-normal distribution where the lowest possible rate is now $-s$ rather than zero. The displacement, $s$, must be sufficiently large that $F+s$ is positive for the lowest forward rate implied by the current term structure. A similar change must be made to the CEV and SABR models. In the option pricing equations $F$ must be replaced by $F+s$ and $K$ with $K + s$ everywhere. In the case of the SABR model, the Black’s model volatility that is calculated is the volatility that applies to the displaced log-normal model with the same displacement, $s$.
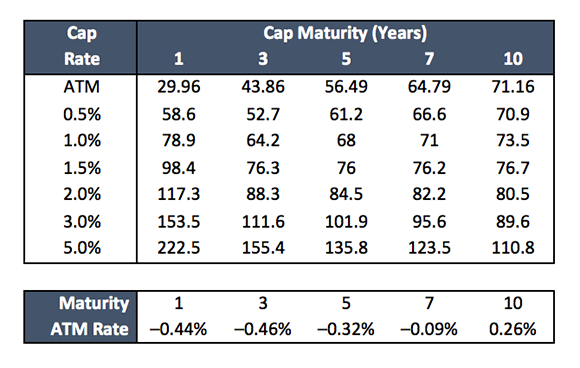
Brokers now adopt one of two approaches. They can switch from Black’s model to the Bachelier model and publish the Bachelier or normal volatility parameters. These are usually expressed in basis points. Alternatively they can use a displaced log-normal model and publish the size of the displacement and the corresponding Black’s volatilities which would be expressed as percentages. The following table shows broker quotes based on the Bachelier model for Euro-denominated caps of various maturities and strikes. The Euro term structure is negative out to about the eight-year point.
Figure 1: Broker quoted normal volatility parameters (in basis points) for caps, with lower panel showing the at-the-money (ATM) cap rates.
 If the broker wants to base the quotes on a displaced log-normal model it is necessary to choose an appropriate displacement. Since the lowest forward rate is about –0.5% the displacement must be at least 0.5%. The following two tables show the displaced log-normal model volatilities that are equivalent to the Bachelier normal volatilities (result in the same cap prices) first for a displacement of 2% and then for a displacement of 1%.
If the broker wants to base the quotes on a displaced log-normal model it is necessary to choose an appropriate displacement. Since the lowest forward rate is about –0.5% the displacement must be at least 0.5%. The following two tables show the displaced log-normal model volatilities that are equivalent to the Bachelier normal volatilities (result in the same cap prices) first for a displacement of 2% and then for a displacement of 1%.
Figure 2: Broker quoted displaced log-normal volatility parameters (%) for caps; Displacement = 2%.
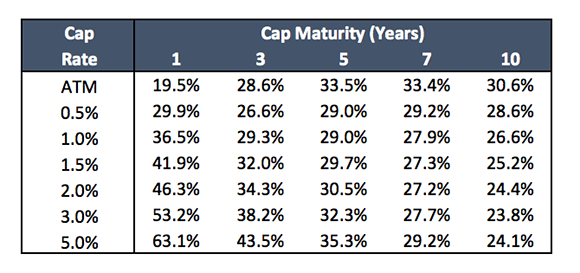
Figure 3: Broker quoted displaced log-normal volatility parameters (%) for caps; Displacement = 1%.

As the size of the displacement is reduced the implied volatilities rise and vice versa. If the displacement is reduced to 0.6% the at-the-money volatilities are larger than 1,000% in some cases. The shape of the volatility surface is also affected by the choice of the displacement value. For 10-year caps higher strikes have higher volatility when the displacement is 1% or 2%. For a very high displacement, the reverse is true, higher strikes have lower volatilities.
The size of the displacement is also important when the SABR model is calibrated to all the options with a particular maturity. Larger displacement values result in a flatter volatility smile which is easier for the SABR model to capture. As a result the pricing errors resulting from the calibration to market data are smaller.
[1] The forward rate will be a three-month rate if we are considering interest-rate caps or a forward swap rate when we are pricing swap options. All the processes for F that we give are martingales. This means that we are implicitly assuming a numeraire equal to a zero-coupon bond with the same life as the option.
[2] Many people are familiar with the Hull-White model in which interest rates are also normally distributed. The Bachelier model for caplets is subtly different from the Hull-White model in that in the Bachelier model it is the rate that has a compounding frequency equal to the accrual period that is normally distributed while in the Hull-White model it is an instantaneous rate that is normally distributed. The result of this is that caplet pricing formulas are different in the two models and Black implied volatility parameters in the two models are slightly different.
[3] See Hagan et al (2002) or Rebonatto, McKay and White (2011).
References
Hull, John, and Alan White. "Pricing Interest-Rate-Derivative Securities." Review of Financial Studies 3.4 (1990): 573-592.
Hagan Patrick S., Deep Kumar, Andrew S. Lesniewski, and Diana E. Woodward, “Managing Smile Risk,” Wilmott Magazine, September 2002: 84-108.
Rebonato, Riccardo, Kenneth McKay, and Richard White. “The SABR/LIBOR Market Model: Pricing, calibration and hedging for complex interest-rate derivatives.” John Wiley & Sons, 2011.
Schachermayer W. and J. Teichmann, J., “How Close Are the Option Pricing Formulas of Bachelier and Black–Merton–Scholes?” Mathematical Finance, 18 (2008): 155–170.
