
In the financial sector, swift progress is being made to prepare for Libor’s end. Global regulators are publishing timelines that are quickly advancing us towards a transition to alternative rates like SOFR, SONIA and €STR.
It is clear that rapid progress has been made for linear products like futures, swaps, bonds, and loans. But there are still a myriad of challenges that must be addressed for non-linear products linked to the Libor benchmark rate, primarily in the case of options like caps, floors and swaptions.
First, I’d like to emphasize that alternative risk-free rate (ARR) options may be uncommon now, but they are growing in popularity. In fact, there are already a few banks dabbling in SONIA swaptions, as well as SOFR futures options. But still uncertainty exists on what these markets will look like. In particular, the question remains, “Will ARR options be cleared, OTC—or both?” Unlike linear products, the nature of interest-rate options will be uncharted territory going forward. Yet we will soon have a mandate to use these options to calibrate the next generation of volatility models.
Updating Volatility Models for ARRs
When we look ahead to the future of volatility modeling, we find a familiar friend in term-structure models, such as the Heath-Jarrow-Morton model (HJM), which can naturally model short-term rates. However, there is likely still work to be done on developing these models specifically for the next generation of ARR non-linear payouts for efficient application.
Interestingly, recent literature has attempted to extend the Libor Market Model (LMM) approach onto in-arrears compounded rates. This shows promise for retaining the simplicity and reuse of previous derivations. But there are some situations where further development is needed, particularly in options trading within the reference period.
Current documentation on the market model approach involves only normal term rate modeling, and it applies a linear volatility decay within the reference period. This is an acceptable approximation, though somewhat ad-hoc and still in detailed disagreement with an accurate HJM model (reference figure below). Conversely, when we look at the shifted LMM and lognormal, we can see very large disagreement with linear vol decay (figure below). Overall this points to a serious need to establish robust volatility decay parameterizations that can reduce this sizeable model risk within the reference period of in-arrears compounded or averaged rates.
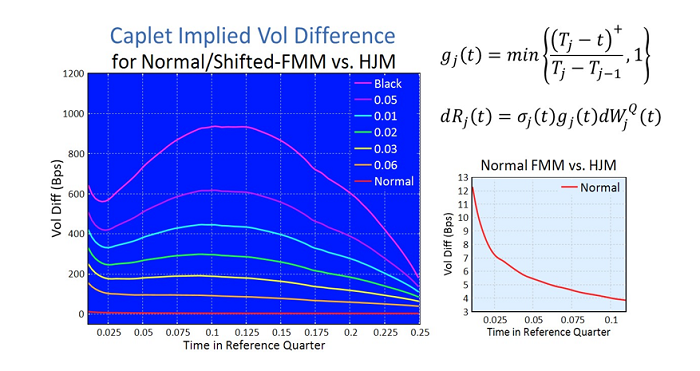
Impacts on Legacy Derivatives
Another point I’d like to emphasize is how Libor fallbacks could apply to non-linear options. On this there has been little to no guidance on from the ARRC or other regulators - most likely due to the lack of a standard master agreement for these products. But I believe this area deserves more attention in order to give market participants some clarity.
Despite the lack of official direction, we can use our best judgement when determining how Libor fallbacks might apply to non-linear options. One example to consider is the Libor-in-arrears convexity adjustment, referenced in the chart below.
Importantly, Libor-in-arrears is unsuitable for an in-arrears fallback, since it pays at the beginning. Therefore, another risk-free term-rate fallback will need to be used. We can derive the original convexity adjustment in the risk-free measure and find it depends on the implied correlation of the risk-free rate and Libor. Thus, it is sensitive to the dynamics of the basis spread.

However, after Libor is phased out, the convexity adjustment will only depend on the variance of the risk-free rate, which will impact the time-value significantly. This impact can be derived under the LMM model and understood to be a combination of the loss of spread dynamics and the impact of the different volatility of the risk-free rate. This conclusion is also applicable to other options, like caps, floors, and swaptions, where the most significant impact from a fallback provision is the large impact on the implied volatility.
Perhaps there is a “smarter” fallback that can account for the forward implied-volatility change. Otherwise there is going to undoubtedly be significant value transfer in non-linear derivatives linked to Libor, which will require cash compensation or re-leveraging when the ill-fated benchmark disappears.
For now, we can only use our best ability to predict the future until more certain terms are clarified for non-linear products. In doing so we can already start to analyze our best-estimate scenarios for the future value of these positions and continue to refine these estimates as the story becomes clear –hopefully in the near future.
For more information on Libor, check out this brief video: The End of Libor

