FINCAD Analytics Suite for Excel and FINCAD Analytics Suite for Developers expand FINCAD's coverage of variance and volatility derivatives by adding functions for the valuation of capped or floored variance swaps.

To download the latest trial version of FINCAD Analytics Suite, contact a FINCAD Representative.

Overview

A variance swap is a forward contract on future realized price variance. It allows investors to take views on future variance (or volatility) without sensitivity to the level of the underlying asset price. Variance swaps can be used to protect against falling markets, since usually volatility (and therefore variance, which is the square of volatility) rises when markets fall. Variance swaps are commonly written on an underlying asset that consists of a basket of assets, such as an index, whereas swaps written on a single stock are almost always capped.

FINCAD Analytics Suite expands FINCAD's coverage of variance and volatility derivatives by adding functions to value capped or floored variance swaps in the Heston model of stochastic volatility.

Capped and Floored Variance Swaps

The issuer of a vanilla variance swap is exposed to unlimited risk, if the volatility of the underlying asset becomes very large. Variance swaps are thus often capped to limit the issuer’s risk.

A capped variance swap with cap C has the payoff

 

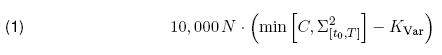
where K_Var is the variance strike and Σ²_[t0,T] is the realized variance during the term of the swap with t₀ being the inception date and T the expiry date of the swap. Analogously a floored variance swap with floor F has the payoff

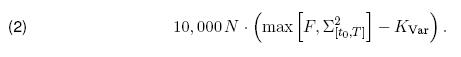
Capped variance swaps protect the issuer from large spikes in volatility. The cap is commonly chosen as 2.5 times the variance strike.

FINCAD Analytics Suite 2010 provides functions to value these swaps in the Heston model:

aaCappedVarianceSwap_Heston_p calculates the price and risk statistics of a capped variance swap.

aaCappedVarianceSwap_Heston_iv calculates the fair strike and risk statistics of a capped variance swap.

aaFlooredVarianceSwap_Heston_p calculates the price and risk statistics of a floored variance swap.

aaFlooredVarianceSwap_Heston_iv calculates the fair strike and risk statistics of a floored variance swap.

Valuation in the Heston Model of stochastic volatility

Vanilla variance and volatility swaps can be valued through a replicating portfolio of European options. The valuation of capped or floored swaps cannot be done without a model for the volatility process, because these swaps depend on the amount of daily variation in the volatility, that is, the variance of volatility. In the Heston model, the variance of volatility ω² is included in the simulation of the variance process.¹ In this model both the price S with drift μ and the variance V follow stochastic processes [1],

where

κ, V₀, V_∞, ω, ρ = the parameters of the Heston model: speed of mean reversion, initial variance, long-term variance, volatility of volatility and correlation.

Pricing capped or floored variance swaps in the Heston model comes down to computing the expected capped or floored variance. The FINCAD Analytics Suite functions implement the quasi-closed form solutions for pricing these derivatives given in [2]. The algorithms require several numerical integrations which render the FINCAD Analytics Suite functions computationally intensive.

Figure 1: Screen shot of aaCappedVarianceSwap_Heston_iv for the calculation of the fair variance.

Example: Pricing a Capped Variance Swap

In this example, we calculate the fair strike for a capped variance swap at its inception. We intend to enter into this swap for a three-month term and a cap which is 2.5 times the initial variance in the Heston model. We found the initial variance and the other parameters for the Heston model via calibration to European options on the equity. Since the initial variance is 0.064, the cap has a value of 0.160.

Given the inputs in Figure 1, we find a fair variance of about 0.061 calculated with the function
aaCappedVarianceSwap_Heston_iv. As a test, we evaluate the fair value using the function
aaCappedVarianceSwap_Heston_p on the effective date, and indeed find that the fair value of the swap is zero.

Summary

FINCAD Analytics Suite coverage of variance and volatility derivatives includes functions to compute fair strikes, prices and all risk statistics for vanilla variance and volatility swaps as well as second and third generation variance derivatives, such as conditional variance swaps and options on realized variance. FINCAD Analytics Suite 2010 expanded this by adding functions for the valuation and computation of all risk statistics of capped or floored variance swaps. As the valuation of capped or floored variance swaps cannot be done without a model for the volatility process, the new FINCAD Analytics Suite functions use the Heston model of stochastic volatility for valuation.

Notes

¹ Strictly speaking, ω² is the variance of variance.

References

[1] Heston, S. (1993), A closed-form solution for options with stochastic volatility, Review of Financial Studies, 6: pp. 327–343.

[2] Sepp, Artur (2007), Pricing Options on Realized Volatility in Heston Model with Volatility Jumps,
Journal of Computational Finance.

For more information or a customized demonstration of the software, contact a FINCAD Representative.

Disclaimer

Your use of the information in this article is at your own risk. The information in this article is provided on an “as is" basis and without any representation, obligation, or warranty from FINCAD of any kind, whether express or implied. We hope that such information will assist you, but it should not be used or relied upon as a substitute for your own independent research.

This document is for informational purposes only. FINCAD MAKES NO WARRANTIES, EXPRESSED OR IMPLIED, IN THIS SUMMARY.