Overview
A payer (receiver) swaption is an option to enter into an interest rate swap wherein a fixed coupon rate is paid (received) upon exercising the option. In case of a European payer swaption, the expiry of swaption coincides with the first rate fixing date of the underlying swap of length ( Tβ - Tα ) where Tα is the swap's first fixing date and Tβ is the swap's termination date. The payer-swaption's discounted payoff to time, t , is given by:
Here,
P(Tα, Ti) is the price of a zero coupon bond at time Tα that terminates at Ti ;
» To evaluate the latest trial version of FINCAD Analytics Suite for free, contact a FINCAD Representative.
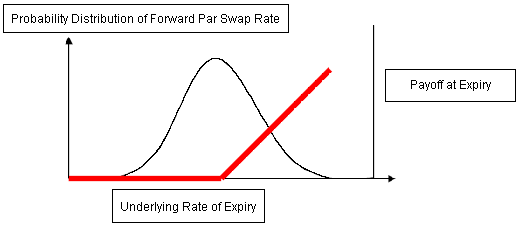
The probability distribution of the forward par swap rate is characterized by the mean and the volatility of the underlying forward rates. A causal chain of reasoning is as follows:
Volatility → Probability distribution of forward par swap rates → Payoff → Swaption price
Different specifications of the forward par swap rate's probability distribution enable one to extract differing swaption prices.
Lognormal Forward Swaption Model:
When the underlying forward par swap rate, Sαβ, is assumed to have a lognormal distribution, the relevant stochastic differential equation is:

It is useful to quickly summarize some key issues arising in the lognormal forward model:
- The distribution of the forward par swap rate is lognormal.
- The standard deviation of the percentage changes in the forward par swap rate is the constant Black-Scholes volatility.
The Normal Forward Swaption Model:
Normalized volatility is the market convention - primarily because normalized volatility deals with basis point changes in rates rather than, as in lognormal volatility, with percentage changes in rates.
The underlying par-swap rate is given by:
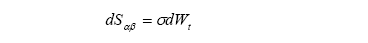
Here, the basis point changes in the forward par swap rates are independent of the level of forward par swap rates involved. The features of the Normal Model are:
- The standard deviation of basis point changes in forward swap rates is a constant normalized volatility.
- There are some realizations of the par-swap rate that can be negative in the normal model; as opposed to the lognormal model where par swap rates are non-negative.
- Since the volatility input for the normal model refers to the volatility for the actual basis point changes - it tends to be smaller than volatility for the lognormal case.
- A useful translation between the lognormal volatility and normal volatility is the following thumbrule:
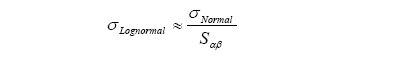
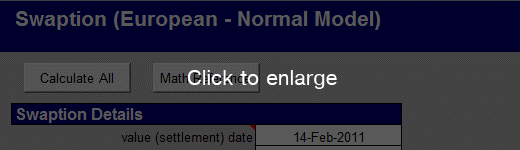
FINCAD Analytics Suite's implementation of Normal Swaption Model:
In FINCAD Analytics Suite, a function named aaNormal_Swaption_fs has been introduced which enables a user to price swaptions where the underlying forward rate is normally distributed. The resultant screen, from a workbook created, is shown here:
The user is expected to input, over and above the standard variables, the rate payment table applicable for the fixed leg and the floating.
References:
- Rebonato, Riccardo (2004). Volatility and Correlation: The Perfect Hedger and the Fox, John Wiley & Sons, England.
- Brigo, D and Mercurio, F (2006). Interest Rate Models: Theory and Practise, Springer Finance, New York.
Disclaimer
Your use of the information in this article is at your own risk. The information in this article is provided on an "as is" basis and without any representation, obligation, or warranty from FINCAD of any kind, whether express or implied. We hope that such information will assist you, but it should not be used or relied upon as a substitute for your own independent research.
» For more information or a customized demonstration of the software, contact a FINCAD Representative.