FINCAD F3 is an enterprise portfolio and risk analytics solution that provides industry standard modeling and analytics with broad asset class coverage and flexibility to model virtually any instrument including complex derivatives such as Corridor Variance Swaps.
FINCAD Analytics Suite includes coverage of variance and volatility derivatives by adding functions for the valuation of next generation variance derivatives, such as conditional variance swaps and options on future realized variance.
Overview
A variance swap is a forward contract on future realized price variance. It allows investors to take views on future variance (or volatility) without sensitivity to the level of the underlying asset price. Variance swaps can be used to protect against falling markets, since usually volatility (and therefore variance, which is the square of volatility) rises when markets fall.
The corridor variance swap and the conditional variance swap are more exotic versions of the vanilla variance swap. In short these next generation variance derivatives accumulate variance only if the price of the underlying asset is within a certain range (the corridor). These instruments provide more flexibility to the investor, as the instrument can be targeted at specific market conditions by selecting the corridor appropriately. A popular instrument is the conditional down variance swap which only accumulates variance if the underlying asset price falls below a pre-determined barrier. This instrument can be very effective in protecting against falling markets. It provides income when the underlying price falls and realized variance rises above the strike but remains at zero value if the asset price stays above the barrier.
Options on future realized variance provide another means for investors to take views on variance. These are options that pay out on the realized variance during the life of an underlying variance swap whose fixed rate equals the strike of the option.
FINCAD Analytics Suite 2009 provides functions to value conditional and corridor variance swaps and options on realized variance in the Heston model of stochastic volatility.
» Click here to start your free trial of the lastest version of FINCAD Analytics Suite!
Conditional Variance Swaps
A conditional variance swap only accumulates realized variance in the floating leg and the fixed variance ("strike") in the fixed leg, if the underlying price is within a pre-determined range. The payoff of a swap with principal P (in units of $ per volatility point squared) and variance strike KVar is therefore
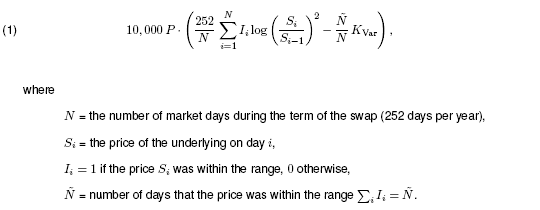
Up and down variance swaps are the two principal types in the market. Up variance swaps only accrue realized variance when the underlying stays above a pre-specified barrier U (i.e. Si > U), whereas down variance swaps only accrue realized variance when the underlying is below the barrier D (i.e., Si ≤ D).
Conditional down-variance swaps are particularly useful to protect against falling markets. The swap remains worthless as long as the underlying price stays above the barrier D, but it accrues variance as markets fall and the investor gains if the variance is larger than the strike. The biggest risk for the buyer of conditional variance is that the underlying price falls below the price barrier, but variance remains small.
FINCAD Analytics Suite 2009 provides functions to value these swaps in the Heston model:
aaCondVarianceSwap_Heston_p calculates the price and risk statistics of a conditional variance swap.
aaCondVarianceSwap_Heston_iv calculates the fair strike and risk statistics of a conditional variance swap.
Corridor Variance Swaps
Corridor variance swaps are very similar to conditional variance swaps; they only accrue realized variance if the underlying price is within a certain range. However, the fixed leg always accrues. Using the notation above, we can write the payoff as
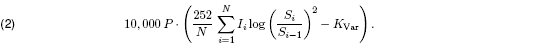
Similar to the conditional down variance swap, a corridor down variance swap can be useful to protect against falling markets, when volatility is large. The biggest risk for the buyer of a corridor variance swap is that the underlying price never enters the range specified in the contract.
FINCAD Analytics Suite 2009 provides functions to value these swaps in the Heston model:
aaCorrVarianceSwap_Heston_p calculates the price and risk statistics of a corridor variance swap.
aaCorrVarianceSwap_Heston_iv calculates the fair strike and risk statistics of a corridor variance swap.
Options on Realized Variance
An option on realized variance gives the holder the right to enter into a variance swap at its expiry. The underlying of this option is therefore the variance that accumulated during the term of the option. The payoff for a call option is
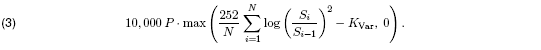
The buyer of a call option gains when realized variance rises above the expected level determined by the strike, but is protected from smaller than expected realized variance. Conversely, the holder of a put option gains when realized variance is below the expected level as determined by the strike, and is protected from large realized variance.
FINCAD Analytics Suite 2009 provides functions to value options on variance in the Heston model:
aaVarianceOption_Heston_p calculates the price and risk statistics of an option on realized variance.
aaVarianceOption_Heston_iv calculates the implied volatility smile for options on realized variance.
Valuation in the Heston Model of stochastic volatility
Vanilla variance and volatility swaps can be replicated with a portfolio of European options. The valuation of the next-generation variance derivatives described above cannot be done without a model for the volatility process, because conditional and corridor variance swaps depend on the price path of the underlying asset and because of the optionality in the option on variance. In the Heston model both the price S with drift and the variance V follow a stochastic process [1],
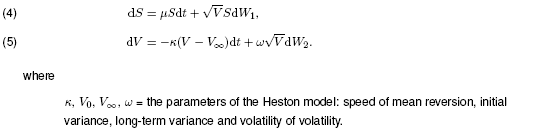
Pricing variance derivatives in the Heston model comes down to computing the expected conditional variance (or optionality in the case of the variance option). The FINCAD functions implement the quasi-closed form solutions for pricing these derivatives given in [2, 3]. The algorithms require several numerical integration which renders the FINCAD functions quite complicated.
Example: Pricing a Conditional Down Variance Swap
In this example, we calculate the fair strike for a conditional down variance swap at its inception. We intend to enter into a conditional down variance with this fair strike for a three month term on a traded equity. At inception, the equity price is $500 and we set the barrier of the swap at $400. For the valuation in the Heston model we calibrated the model parameters using European options on the equity.
We use the FINCAD workbook "Corridor or Conditional Variance Swap (Heston Model)" for our calculations. Figure 1 shows the inputs for this example on the worksheet "Main". Given the inputs in Figure 1, we find a fair variance of 0:179 which was calculated with the function aaCondVarianceSwap_Heston_iv. Evaluating the fair value using the function aaCondVarianceSwap_Heston_p on the effective date, we indeed find that - up to rounding errors in the fair variance - the fair value of the swap is zero.
On December 22, 2008, we use aaCondVarianceSwap_p to compute the present value of the conditional variance swap we bought. We enter the price path of the asset for the past 19 market days on the worksheet "Realized Var". Given the particular path, we find that the asset was below the barrier on eight out of the 19 days and that the realized conditional variance is 0:221. These values are linked to the worksheet "Main" and we proceed to compute the fair value on December 22, 2008 by only changing the value date on the worksheet. The function returns the fair value in the section "Results - Fair Value" to be about $493,000.
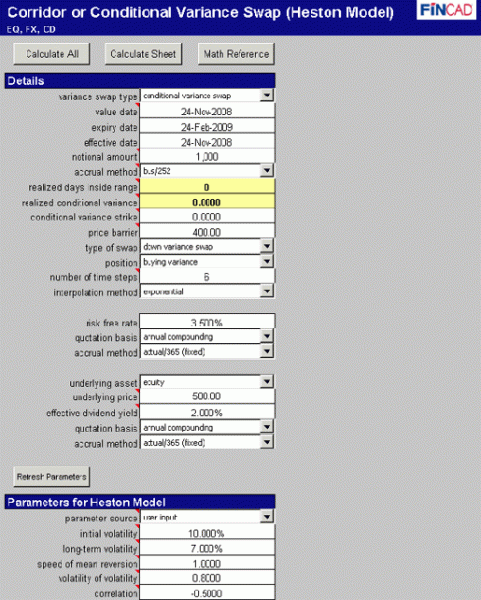
Figure 1: Screen shot of the inputs to aaCondVarianceSwap_Heston_iv for the calculation of the fair variance.
Summary
FINCAD Analytics Suite 2009 provides functions to compute fair strikes, prices and all risk statistics for vanilla variance and volatility swaps as well as second and third generation variance derivatives, such as conditional variance swaps and options on realized variance. As the valuation of these more recent instruments cannot be done without a model for the volatility process, the new FINCAD functions use the Heston model of stochastic volatility to value these instruments.
References
[1] Heston, S. (1993), A closed-form solution for options with stochastic volatility, Review of Financial Studies, 6: pp. 327-343.
[2] Sepp, Artur (2007), Pricing options on realized volatility in heston model with volatility jumps, Journal of Computational Finance.
[3] Sepp, Artur (March 2007), Variance swaps under no conditions, Risk, pp. 82-87.
For more information or a customized demonstration of the software, contact a FINCAD Representative.
