FINCAD Analytics Suite offers valuation of variance and volatility swaps both with model-independent replication strategies, and within the Heston Model. To download the latest trial version of FINCAD Analytics Suite for free, contact a FINCAD Representative.
Overview
The classic derivatives that allow investors to take a view on volatility are straddles or strangles. A long position in a straddle, for example, will generate a profit if the underlying asset price moves up or down, or if the implied volatility rises. However, these options are also sensitive to the underlying asset price, as the delta of a straddle or a strangle is zero only when the option is at-the-money.
Unlike these options, variance and volatility swaps provide pure exposure to volatility. A volatility swap is essentially a forward contract on future realized price volatility. At expiry the holder of a long position in a volatility swap receives (or owes if negative) the difference between the realized volatility and the initially chosen volatility strike, multiplied by a notional principal amount. A variance swap is analogously a forward contract on future realized price variance, which is the square of future realized volatility.
In both cases, at inception of the swap the strike is chosen such that the fair value of the swap is zero. This strike is then referred to as fair volatility and fair variance, respectively.
Variance and volatility swaps can be used to speculate on future realized volatility, to trade the spread between realized and implied volatility, or to hedge the volatility exposure of other positions. For example, variance swaps can effectively protect against drops in the underlying price: since volatility is generally negatively correlated with the underlying price, a long position in a variance swap will generate a gain, if the underlying price drops sharply.
Variance swaps can be replicated and valued in a model-independent manner, using a static portfolio of European vanilla options [1]. For this reason, variance swaps are more popular than volatility swaps - for which there exist only approximate static replication strategies. On the other hand, both types of swaps may be valued within a calibrated Heston model [2].
Replication with Vanilla Options
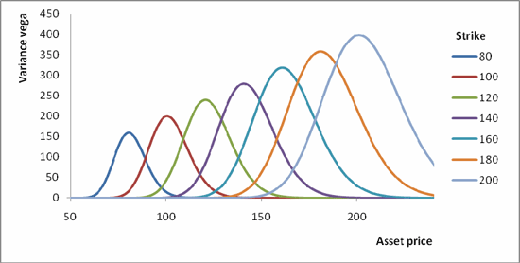
The variance swap replication is accomplished using a portfolio of options with different strikes. The construction of this portfolio can be understood intuitively in the Black Scholes model.1 The sensitivity of a European option to the variance of the underlying asset price depends on the asset price. This "variance vega"2 is largest when the underlying price is closest to the strike of the option, and is also an increasing function of the strike. Both these dependencies are illustrated in the graph below, which shows the variance vega as a function of the underlying asset price for a range of strikes.
Figure 1: Variance vega for individual vanilla call option
The variance vega of a portfolio of options that replicates the variance swap payoff must be independent of the underlying price. To achieve this, each option has to be weighted by the inverse of the strike squared. The following graph shows the variance vega of such a portfolio: the sum of the above options, weighted appropriately. As can be seen, the variance exposure of the portfolio is largely independent of the underlying asset price, as long as the price lies within the range of option strikes.
Figure 2: Variance vega for a portfolio of vanilla options
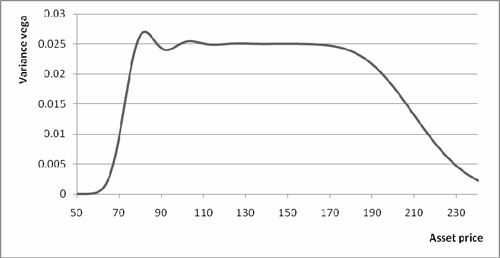
In fact, as the spacing between strikes is decreased and the range of strikes in the options portfolio increases, the variance exposure becomes entirely independent of the underlying stock price. The rigorous derivation given in [1] shows that such a portfolio indeed replicates the payoff of a variance swap.
The FINCAD Analytics Suite function aaVarianceSwap2_port can be used to approximate a variance swap with a finite number of options. From an input volatility smile table that lists the available options, the function computes the value of each option and the number of options at each strike required in the portfolio. On the other hand, the functions aaVarianceSwap2_iv and aVarianceSwap2_p compute the fair variance and the fair value of a variance swap, respectively.
The replication of a volatility swap is not as simple as that of a variance swap. Variance arises naturally in the P&L of hedged options, which depends linearly on variance. Volatility on the other hand should be viewed as a derivative of variance. As volatility is the square root of variance, the relation is non-linear, which does not allow replication by a static options portfolio. An approximate strategy replicates a volatility swap with unit notional by a variance swap with notional of 1/(2.Kvol), where Kvol is the volatility strike of the volatility swap.
FINCAD Analytics Suite provides the functions aaVolatilitySwap_port, aaVolatilitySwap_p and aaVolatilitySwap_iv for calculating the approximate replicating portfolio, the fair value and the implied volatility, respectively.
Valuation in the Heston Model
The replication strategies discussed above are largely model-independent, as they only assume that the underlying asset price process be continuous. However, given some model of the underlying asset price dynamics, variance and volatility swaps can also be priced. A natural model to use is the Heston model of stochastic volatility. In this model the underlying asset price S follows a standard lognormal process, and the variance V follows a mean-reverting square root process:

where r is the risk-free interest rate, we have ignored dividends, and dW1 and dW2 are two (correlated) standard Brownian motions. The five Heston model parameters are: the initial variance V0, the long-term variance Vϖ, the speed of mean reversion K, the volatility of volatility ϖ, and the correlation ρ.
For the valuation of a variance swap, the expected total variance E[∑2] over the term of the swap has to be calculated. In the Heston model this expectation value follows from the differential equation for the variance process given above [2]:

Similarly, the expected total volatility required for the valuation of a volatility swap can be computed in the Heston model. However, the expression is more complicated than the variance expectation and its calculation involves a numerical integration [2].
FINCAD Analytics Suite provides the functions aaVarianceSwap_Heston_p, aaVarianceSwap_Heston_iv, aaVolatilitySwap_Heston_p, and aaVolatilitySwap_Heston_iv for the fair value calculation and for the calculation of the implied variance and volatility for variance and volatility swaps respectively.
In addition, FINCAD Analytics Suite includes the functions aaCalibrateVarianceSwaps_Heston and aaCalibrateVolatilitySwaps_Heston, which can be used to calibrate the Heston model parameters to the term structure of variance and volatility swaps respectively.
Example: Model-independent Valuation with a Replicating Portfolio
In this example we use the FINCAD Analytics Suite workbook "Variance or Volatility Swap" to calculate the replicating portfolio for a variance swap and its fair variance which would result in a zero fair value of the swap at inception. We also calculate the fair value of the swap some time after inception. For the replication we have ten options that we enter in the worksheet "Smile Table":
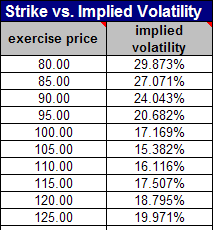
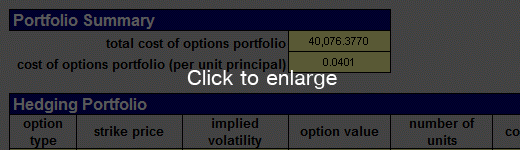
We enter the variance swap contract on March 3, 2008 with expiration on May 2, 2008, a notional amount of $100 per volatility point squared, a variance strike of 0.04, corresponding to a volatility of 20%, and an accrual method of bus/252, counting only market days. The annually compounded risk free rate is 3.5% and the underlying asset price is $100 with a dividend yield of 0%. Using the input volatility smile table the replicating options portfolio is calculated on the worksheet "Portfolio":
The first column in the "Hedging Portfolio" table lists the type of options required at the strike price given in the second column. The implied volatility in the third column follows directly from the given smile table. The fourth column is the option's value as computed in the Black Scholes model. The replicating portfolio is given in the fifth column, which lists the number of put and call options that are required at each strike. The final column is the price of the position in each option. Clearly, the positions of the at-the-money options are the most expensive. The total value of the portfolio is the sum of all option position prices and amounts to about $40,000 for this variance swap.
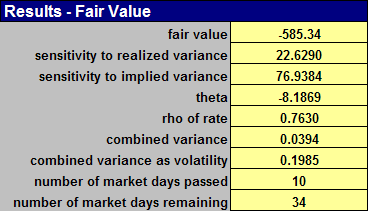
We now calculate the fair variance and the associated risk statistics for the variance swap using the worksheet "Fair Var". The result is

The fair variance is close to the variance strike. The delta of the variance swap is very small; it is different from zero, because the replication with just ten options is not perfect.
After two weeks we compute the present value of the variance swap. For simplicity we assume that all inputs including the volatility smile are the same, except for the value date which is now March 17. On the worksheet "Realized Var" we enter the realized prices for the two week period and calculate the realized variance, which is 0.039 corresponding to a volatility of 19.7%.
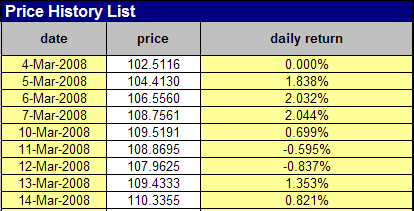
The realized variance (0.039) is slightly smaller than the variance strike (0.040) of the swap. The implied variance on the value date that follows from the options portfolio is 0.0395. The present value of the swap is therefore slightly negative:
Example: Valuation in the Heston Model
We now evaluate the fair variance of the variance swap in the Heston model with the function aaVarianceSwap_Heston_iv. On the effective date (March 3), the Heston parameters corresponding to the volatility smile given in the example above are an initial volatility of 19%, a long-term volatility of 25%, a speed of mean reversion of 1, a volatility of volatility of 100%, and a correlation of -0.5. For the calculation we use the FINCAD Analytics Suite workbook "Variance or Volatility Swap (Heston Model)". We enter the variance swap details on the worksheet "Main" as shown in the following screenshot.
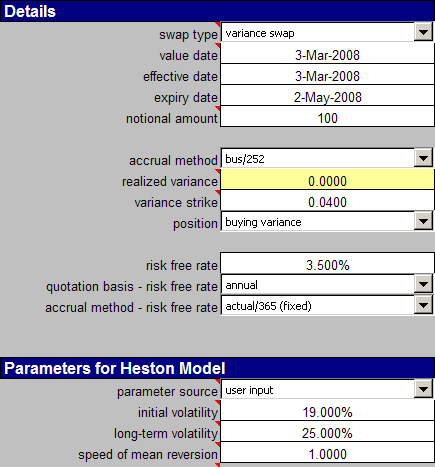
Note that the valuation of a variance swap in the Heston model does not depend on the volatility of volatility or on the correlation. The fair variance of the variance swap evaluates to 0.383 or 19.564% in units of volatility. This value is close to the value we calculated with the options portfolio replication strategy in the first example, as should be expected. One would find exact agreement only for a perfectly calibrated model and an options portfolio with continuous strikes.

Summary
FINCAD Analytics Suite provides functions to value variance and volatility swaps using model-independent replication strategies as well as using the Heston model. The former functions allow the user to compute portfolios that replicate the floating leg of a variance swap. Based on this replication strategy, the fair variance and the fair value including all risk statistics can be calculated. If the user has calibrated the Heston model to European options or to variance or volatility swaps, the Heston model functions can be used to compute the fair variance and the fair value of a variance or a volatility swap.
1 The mathematical derivation does not assume Black Scholes dynamics, but only requires that the price process of the underlying asset be continuous, that is free of jumps.
2 Variance vega is the derivative of the option price with respect to variance, or equivalently to the volatility squared.
References
[1] Demeterfi, K., Derman, E., Kamal, M. and Zou, J. (1999) 'A Guide to Volatility and Variance Swaps', Journal of Derivatives, 6, 9-32; 'More Than You Ever Wanted to Know About Volatility Swaps', Goldman Sachs Quantitative Strategies Research Notes, March 8, 1999.
[2] Gatheral, J. (2006) 'The Volatility Surface: A Practitioner's Guide', Wiley Finance.
Disclaimer
Your use of the information in this article is at your own risk. The information in this article is provided on an "as is" basis and without any representation, obligation, or warranty from FINCAD of any kind, whether express or implied. We hope that such information will assist you, but it should not be used or relied upon as a substitute for your own independent research.
For more information or a customized demonstration of the software, contact a FINCAD Representative.